Description
Letbe the sum of positive proper divisors
of . For example, and Let Given , find .
First line contains ), the number of test
cases. Each of the next lines
contains a single integer . )
Output
For each number , output a
single line containing .
1
2
3
4
5
6
7
| 6
1
2
3
10
100
1000000000000000000
|
Sample Output
1
2
3
4
5
6
| 0
1
2
32
3249
322467033424113218863487627735401433
|
洛谷题面
Solution
题意即求的前缀和
现在问题就是求
相当于是求双函数在到时下方的整点数
借用一下这位老哥的图以及题解
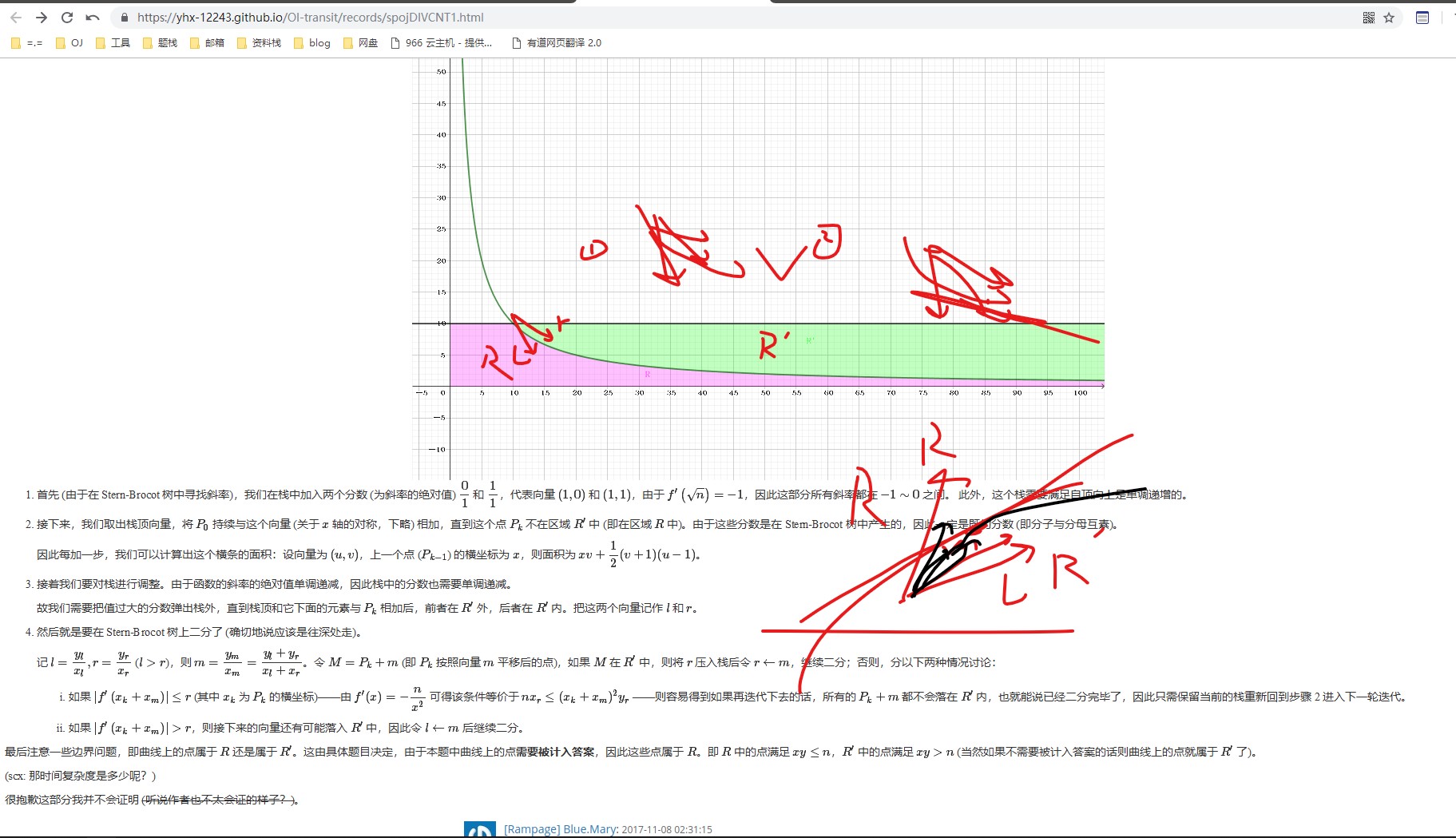 SPOJ26073
SPOJ26073
可以看出是要求紫色部分(以下称为"R区域")的整点个数
然后可以使用一个叫做树的东西(我也不会,想学自己去查吧=.=)
只需要知道它可以不重不漏的构造出所有的真既约分数
然后我们从点出发(在R区域上方),初始添加分数和,每次按照着那个树构造出的分数作为向量往下走直到走到R区域(就不走这一步了),然后在树(???)上二分出(不知道叫不叫二分,可能也不叫)下一步走的向量,答案加等于然后一直这样走,直到最后走到时每次基本都是向右走很多$ y$)可以直接暴力,然后就完了。
????
不是故意题解写成这样的,是膜X的后遗症
Q1:为啥初始点坐标?
A1:我们要求R区域内的整点个数(包括边界),可能可以从边界上开始算,但感觉要判是不是平方数什么的,细节很多,直接从R区域上方开始,每次找到一个尽可能贴近双曲线的向量(但不相交)顺着走,这样只需考虑当前点左边的点(不包括自身)可能会好写一些,坐标是之后往下走的时候默认当前坐标所在行已经算过答案了,如果不的话就会少 时的答案
Q2:每次往下走之后答案多了哪些点呢?
A2:好问题!因为我也想了半天那个是哪里冒出来的,然而网上题解大概就两篇,不知道是不是一个人写的都没解释,拿出画图:
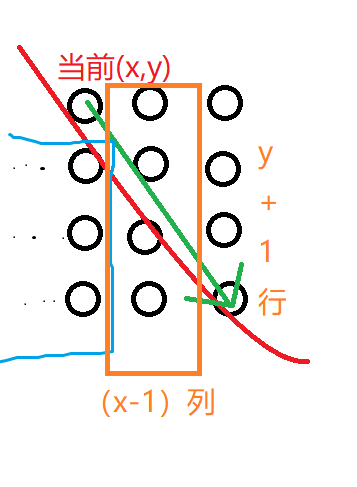 SP26073.png
SP26073.png
红色部分是双曲线,因为我们找到的是最贴合双曲线的向量(图中绿色),所以绿色一定不会经过其他的点(否则向量就是上面的点到这个“其他的点”了),新增的点的个数就是蓝色部分+橙色部分在R区域内的点数(我们的当前点以及走到的点都在R区域外,都不计入答案),由图像可知蓝色部分点数是, 橙色部分点数是对称的,(不对称则向量会到不对称的那个点)所以橙色部分在R区域内的点数=
Q3:怎么找到最贴近双曲线的向量?
A3 :因为我们要向量,树给我们提供的是向量的斜率的绝对值,所以为了避免难写,维护的是向量的绝对值的一个栈。相当于把最上面那个图上下翻转一下,然后维护一个从栈顶到栈底斜率越来越低的栈,如果按之前的方法走的向量再走一遍就到R区域了,那么就一直弹栈直到当前的在R区域而
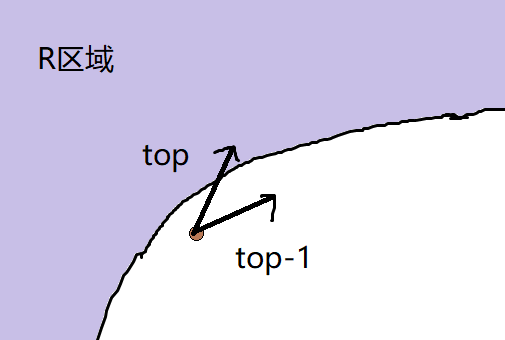 Q3_1.png
Q3_1.png
就像这样
把记为,记为按照树的方法生成他们的合向量,然后分两种大的情况讨论
Case1:
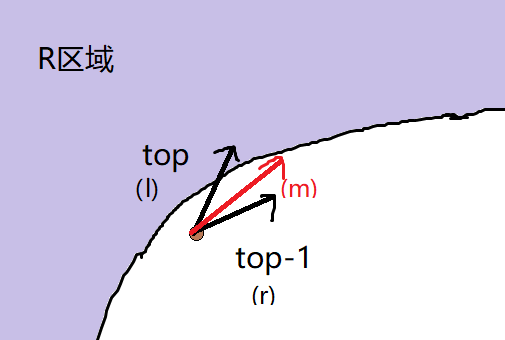 Q3_2.png
Q3_2.png
当前点走不会走进R区域
所以一定比更贴近双曲线,可以令再继续二分
Case2:
 Q3_3.png
Q3_3.png
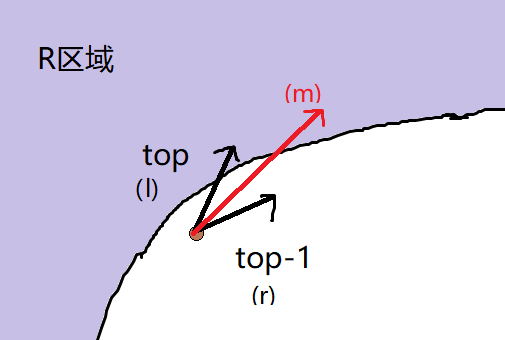
如果走会到R区域内
那么分的斜率和双曲线在的斜率的大小关系讨论
-
试想一下之后如果之后继续二分,得到的的比现在的还要大,那么双曲线斜率就还要小,不管变得多么接近斜率仍永远比双曲线的大,所以仍一定在R区域内(或者可以考虑二分的过程,相当于是每次,而双曲线在处已经斜率小于等于了,所以无论之后加多少个仍然在R区域)直接
break掉
-
那么之后加若干还是可能走出区域的,就令再继续二分
代码里写的是用的斜率,当然也可以求导得到等价的不用double的表达式
Q4:所以那个树有啥用啊?
A4:emmm...可能是能够保证这样一定能够造出所有斜率,不会漏解,然而直觉上感觉是对的就行了
Q5:咋暴力啊?
A5:该怎么暴力就怎么暴力
Q6:时间复杂度?
A6:不会证,参见IOI2018候选队论文《一些特殊的数论函数求和问题
朱震霆》
Q7:为啥你和哪位老哥代码那么像?
A7:因为是抄的啊
注意答案可能爆long long, 要_int128
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
| #include<bits/stdc++.h>
#define ll long long
#define lll __int128
#define FIO "SP26073"
using namespace std;
const int N=1e7+5;
struct point{
ll x,y;
inline point(ll _x=0,ll _y=0){x=_x;y=_y;}
inline point operator +(const point &t)const{
return point(x+t.x,y+t.y);
}
}st[N],L,R,M;
ll n;
inline bool inR(ll x,ll y){return x*y<=n;}
inline double slope(ll x){return (double)n/x/x;}
inline lll s0(){
lll ret=0;
int t=0,rt=cbrt(n);
st[++t]=point(1,0);
st[++t]=point(1,1);
ll m=sqrt(n),x=n/m,y=m+1;
while(1){
for(L=st[t--];!inR(x+L.x,y-L.y);x+=L.x,y-=L.y)
ret+=x*L.y+(L.y+1)*(L.x-1)/2;
if(y<=rt)break;
for(R=st[t];inR(x+R.x,y-R.y);R=st[--t])L=R;
while(1){
M=L+R;
if(!inR(x+M.x,y-M.y))st[++t]=(R=M);
else{
if(slope(x+M.x)<=(double)R.y/R.x)break;
L=M;
}
}
}
for(int i=1;i<y;i++)ret+=n/i;
return ret*2-1ll*m*m;
}
int T;
inline void write(lll x){
if(x>=10)write(x/10);
putchar(x%10+'0');
}
inline void writeln(const lll &x){
write(x);
putchar('\n');
}
int main(){
freopen(FIO".in","r",stdin);
freopen(FIO".out","w",stdout);
scanf("%d",&T);
while(T--)scanf("%lld",&n),writeln(s0());
return 0;
}
|




