一、计算机动画
动画：运动（活动）的画面（图像）
- 动画是通过连续播放一系列画面，给人的视觉造成连续变化的效果
- 二维动画：通过设计和绘制二维图形或图像而生成的动画
- 三维动画：通过构造并直接控制三维模型运动而生成的动画
动画片的基本原理和基本概念
- 视觉暂留原理：人的眼睛看到一幅画或一个物体后，大约在
秒内不会消失 - 利用视觉暂留原理，在一幅画还没有消失前播放下一幅画，就会给人造成一种流畅的视觉变化效果
- 帧：动画中每幅画
- 现在电影的播放速度：24 帧/秒
计算机动画是图形学和艺术相结合的产物。它综合利用计算机科学、艺术、数学、物理学和其它相关学科的知识用计算机生成绚丽多彩的连续的虚拟真实画面。
- 给人们提供了一个充分展示个人想象力和艺术才能的新天地。
- 计算机动画得以迅速发展，并形成一个巨大的产业，与影视、游戏的重大需求和推动是密不可分的。
计算机动画应用
- 影视动画片
- 影视特效动画
- 广告动画
- 游戏动画
- 医疗卫生
- 科学可视化以及教育
- 军事训练和作战演习模拟
二、三维对象的表示
边界表示法
多面体
多面体表示–使用一组包围对象表面的多边形
- 三维图形建模中运用边界表示是最普遍的形式
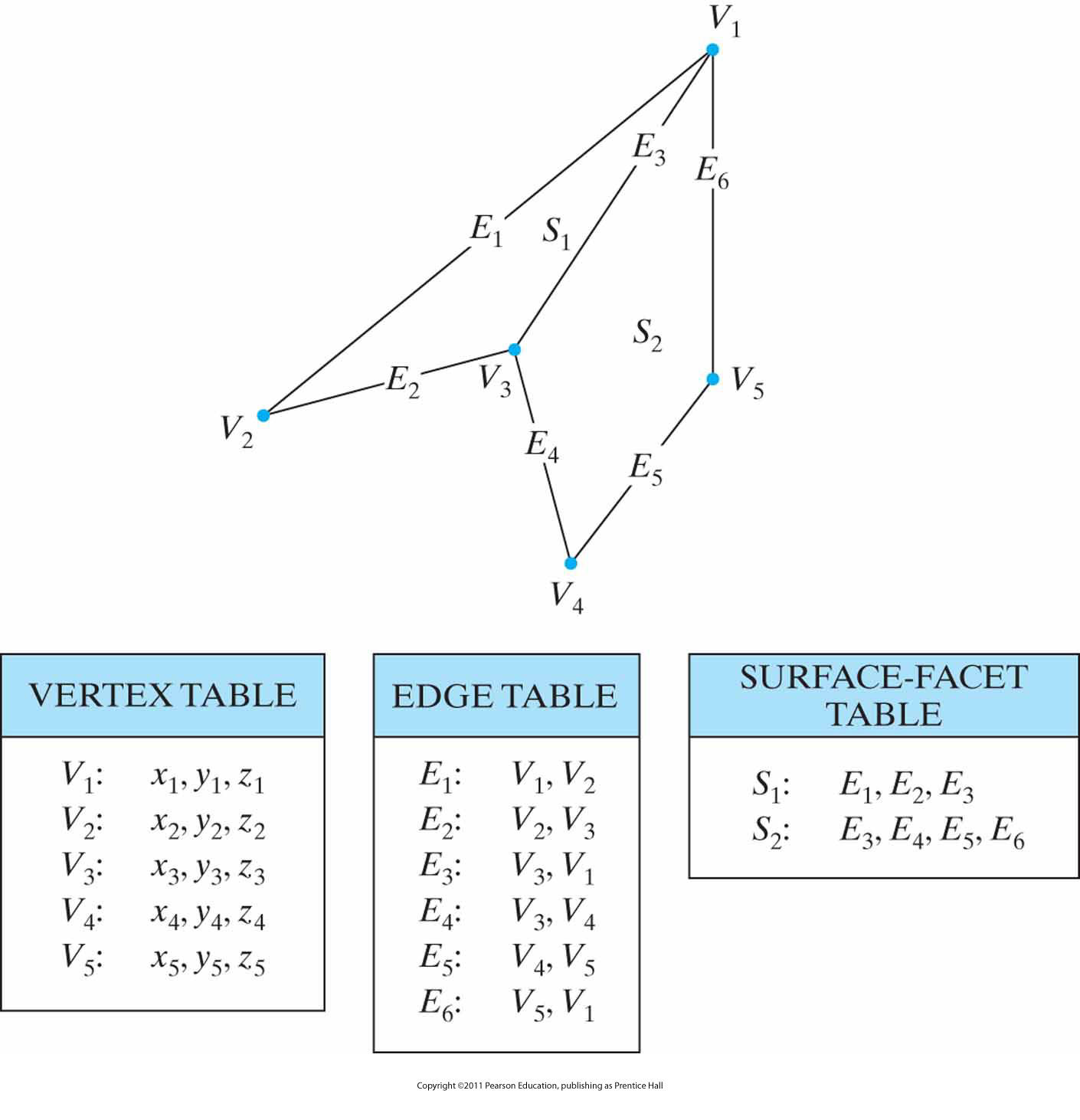
边界表示方法：
- 为覆盖对象表面的每一多边形给出一组顶点
- 顶点坐标和边的信息以及多边形表面法向量等其他信息存入一张表中
多边形的几何数据：
- 顶点表
- 边表
- 面片表
曲面
二次曲面（quadric surface） –表面使用二次方程进行描述
常见二次曲面：
- 球面
- 椭球面
- 环面
- 抛物面
- 双曲面
超二次曲面
超二次曲面是二次曲面的一般化表示
- 超二次曲面通过将额外参数插入二次方程而形成，便于调整对象的形状
- 常见超二次曲面：
- 超椭圆
- 超椭圆球
样条表示
样条–通过一组指定点集而生成平滑曲线的柔性带
样条曲线（spline curve）-由多项式曲线段连接而成的曲线，在每段的边界处满足特定的连续性条件
样条曲面（spline surface）-通过两组样条曲线生成
应用：
- 设计曲线和曲面形状、对象的动画路径
- 典型计算机辅助设计：汽车车身设计、飞机和航天机表面的设计、船体设计
通过控制点可得到曲线的大致形状
插值样条曲线（interpolate）-曲线通过每个控制点
用于数字化绘图或指定动画路径
逼近样条曲线（approximate ）-部分或者全部控制点不在生成的曲线上
作为设计工具来构造对象形体
凸壳
凸壳（convex hull）-包含一组控制点的凸多边形边界
凸壳的作用：
给出了曲线或曲面的坐标范围
样条以凸壳为界，保证了对象形态平滑地沿控制点前进
参数连续性条件
- 0 阶参数连续性 C0-曲线相连
- 1 阶参数连续性 C1-两条相邻曲线段的方程在相交点处有相同的一阶导数
- 交点处有相同的切线
- 2 阶参数连续性
C2-两条相邻曲线段的方程在相交点处有相同的一阶和二阶导数
- 交点处的切向量变换率相同
三次样条插值方法
- 思路：给出一组控制点，利用三次多项式拟合每对控制点之间的曲线，通过设置两条曲线段交点处平滑条件求解得到所有系数
- 为什么用三次多项式？
- 计算效率：需要较少的计算和存储空间，并且较为稳定
- 灵活性：可模拟任意曲线形状
- 作用：多用于建立对象运动路径或提供实体表示和绘画，也可用于设计物体形状
Bézier曲线
线性 Bézier 曲线
给定点
二次 Bézier 曲线
二次 Bézier 曲线的路径由给定点控制点
三次 Bézier 曲线
三次贝塞尔曲线的路径由给定点控制点$$
递归定义方式
混合函数
Bézier 曲线性质
- Bézier 曲线总是落在控制点的凸壳内
- 混合函数值为正且其总和为
Bézier曲面
使用两组正交的 Bézier 曲线设计一个曲面
B 样条
- B 样条多项式次数可独立于控制点数目
- B 样条允许局部控制曲线或曲面
- B 样条比 Bézier 更复杂
实体构造法
扫描表示法
扫描表示法–通过平移、旋转及其他对称变换来构造三维对象
方法：指定一个二维形状，在空间区域内移动该形状
路径：
- 描述路径的曲线函数
- 沿路径移动的距离
形状：
沿扫描线改变剖面的形状和大小
平移扫：垂直于二维集合进行扫过
旋转扫：绕某一轴线旋转某一角度
广义扫：二维几何集合沿一条空间曲线的集合扫过
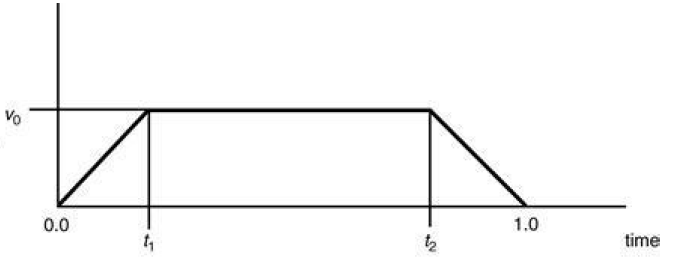
结构实体几何法
使用集合操作（并、交或差操作）来组合多个三维对象
空间分区表示
定义
- 描述内部性质，将包含一个对象的空间区域划分成一组较小的、非重叠的连续实体
常用于三维医学成像
八叉树
- 八叉树（octree ）-分层树形结构，用于显示对象内部结构
- 每次使用与笛卡尔坐标平面对齐的三个相互垂直的平面对场景进行分割
- 构造出树形结构后，要求每一个结点对应于一个三维空间区域
- 构造
- 将三维空间区域分成八等份，并且在树上的每个节点处存储8个数据元素（体元）
- 每个体元若为一个均质子区域，则存储该子区域的特征值，如颜色、材质、密度等
- 否则，需进一步分解为8个子立方体
- 分解直至所有小立方体单元均质，或已分解到规定的分解精度为止
- 优点
- 提供了存储有关物体内部信息的方便表示
- 利用了空间相关性，减少了三维物体的存储需求
BSP 树
BSP 树-二叉空间分割树（Binary space partitioning），每次将空间分成两部分 自适应空间细分，每次将一个场景根据适合于对象空间分布的平面分成两部分 优点：
- 减少场景树的表示深度
- 减少了搜索树的时间
基于物理的建模方法
基于物理的建模–对象形状和表面特征随着对象运动或受到邻近物体影响而改变
非刚性物体，如绳、布料或软橡皮球使用基于物理的建模
另外，流体，如水流、烟雾的建模
三、关键帧动画
基本概念
关键帧动画技术是传统动画和计算机动画制作的常用技术
关键帧（原画）-动画制作过程中，由动画设计师绘制出动画的一些关键画面
- 一般需要很高的经济成本，而且要求动画设计师具有丰富的经验
中间插画制作–在关键帧之间需要补充插入一些画面，使得关键帧能够连贯起来
- 一般远远低于关键帧制作的经济成本，通常由助理动画师或者其他美术人员或者计算机自动完成
关键帧动画技术-研究如何制作填充与关键帧之间的画面，使得整个动画更加合理流畅
实现方法：插值技术
插值对象：
- 空间数据
- 对象的颜色、透明度
- 相机的焦距
线性插值
设物体在第 1 个关键帧中的位置为
线性插值（颜色）
设物体初始颜色值为
非线性插值
中间帧变化模式为非线性：
- 插值样条
- Hermite插值等
- 逼近样条
- Bézier样条
- B样条
利用二次Bézier曲线进行关键帧插值 点
控制插值点移动速度
通常需要通过确定中间帧的帧数来控制过渡的时间以及表现角色的运动快慢和精神面貌等
- 如果中间帧的帧数较少，则通常具有较快的运动速度
- 如果中间帧的帧数较多，则通常具有较慢的运动速度
目标：如何使得对象按照用户确定的移动特性在指定轨迹上运动：即建立从时间t 到对象坐标位置p 的关系
求得对象移动的路径长度s与路径方程参数u的关系：
进而推导出特定弧长s所对应的u值：
- 设定对象移动的路径长度s与时间t关系：
求得对象移动的路径长度s与路径方程参数u的关系
方法：
- 解析求解方案-任意空间点之间弧长通过积分求解 大多数曲线不适用
- 数值求解近似求解
- 对曲线进行超采样进而构造一个表格记录弧长与参数的关系
- 通过高斯求积估算弧长
弧长计算方法-前向差分法
对参数
和弧长 进行采样：如 取 ，得到不同采样点 通过计算邻接顶点间的线性距离，逼近弧长
创建一个路径长度
与路径方程参数 的关系表：
| 索引 | 路径方程参数值 |
路径长度 |
|---|---|---|
| 0 | 0.00 | 0.000 |
| … | … | … |
| 8 | 0.40 | 0.720 |
| 9 | 0.45 | 0.800 |
| … | … | … |
| 14 | 0.70 | 0.944 |
| 15 | 0.75 | 0.959 |
已知
求对应的 求
时曲线弧长 已知
求对应的 求弧长
对应的参数
优点：
易于实现、直观且具有较高的计算速度 缺点：
弧长以及参数值的插值计算将在一定程度上引入误差
解决方法：
- 对曲线实施超采样，从而减少误差的产生
- 修改插值方案，采用高阶插值计算降低误差，但增加了计算复杂度
- 应在速度和精度之前作出某种权衡
速度控制-实现易入易出
速度控制
- 匀速运动
- 自定义
- 常见：易入/易出（ease-in/ease-out）：对象从静止位置处加速运动并达到最大速度，最终减速运动至静止处
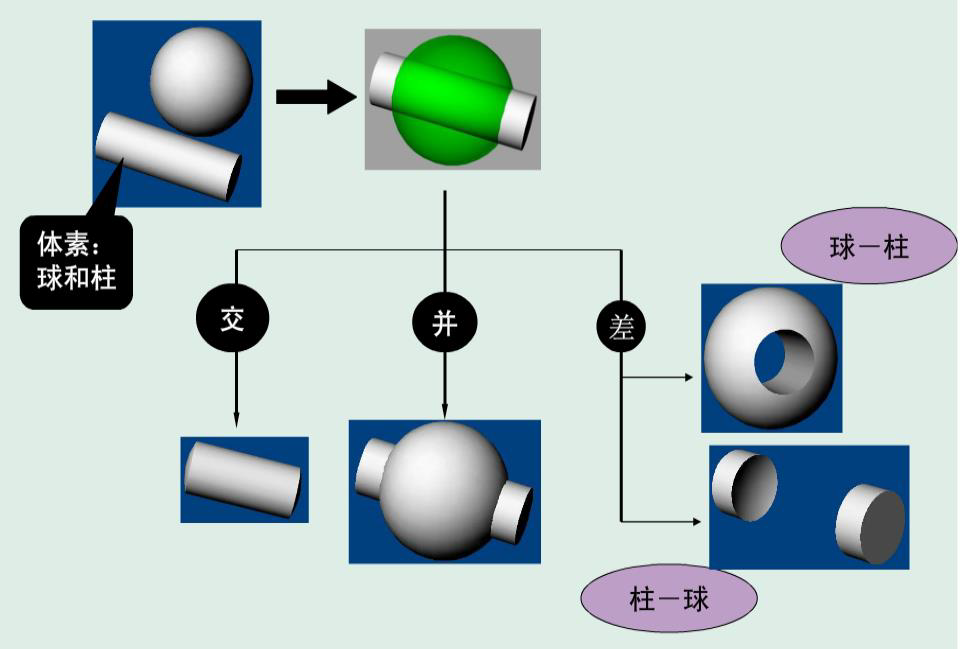
距离-时间函数
- 距离-时间函数在
上呈现出单调性 - 距离-时间函数在
上保持连续性
实现易入/易出移动控制特性的方法
正弦插值
使用正弦曲线
作为实现方案 将
映射到 将函数范围
映射到 运动方式：缓慢启动、加速、减速 由于斜率处于不断变化中，因而移动过程中呈现出加速或减速状态 很少呈现匀速状态 正弦片段+直线
用户定义数据值
和 ，希望物体在 实现加速运动， 实现匀速运动， 实现减速运动 通过整合正弦曲线段和直线完成
正弦曲线 直线 正弦曲线 归一化：每项除以
一元三次多项式
缺点：未提供匀速的控制方式 均匀加速度
最简单的非易入/易出模型
- 加速度为0
- 速度恒定
易入/易出模型
- 假设加速度开始和结束阶段非零
- 中间阶段加速度为零
- 基于正弦函数方案实现起来较为直观
- 但与加速度-时间函数以及速度-时间函数比，该方案缺乏灵活性
- 加速度-时间函数以及速度-时间函数可使用户对最终的移动效果具有较好的控制力
变形的基本思想
变体（变形）（Morphing）–关键帧技术重要的手段
- 变体是已知源对象和目标对象的前提条件下构造一系列中间对象，从而使得从源对象通过这些中间对象光滑地变化到目标对象
- 图像变体：如果源对象和目标对象是两幅二维的图像
- 图形变体：如果源对象和目标对象是由图形组成
不论是图像变体还是图形变体，都是使对象形状变形–形状之间的转换操作
多数动画设计人员通常需要对形状实施精准控制：
- 确定对象的关键形状
- 关键形状之间采用插值计算完成，进而生成形状之间的平滑变换
主要思想：
- 确定对象上每个点相对于局部坐标系统的坐标
- 对局部坐标系统实施变形操作
- 将对象上每个点重新映射到新的局部坐标系统
基于网格的图像变体技术
目标
设源图像和目标图像分别为
- 当
时， ；当 时， ； - 当
从 匀速地变换到 时，中间帧图像 从图像 逐渐变换到
方法
为图像
和 建立在拓扑上的一一对应的四边形网格 通过交互方式，分别为图像
和 选取特征点，使得图像 的特征点和图像 的特征点一一对应 连接图像
的特征点形成四边形网格，连接图像 的特征点形成四边形网格图像 的四边形网格和图像B的四边形网格存在一一对应关系 每个四边形网格为一个独立的局部坐标系
中间帧图像的四边形内部及边界上的点
定义为两次线性插值 中间帧图像的四边形网格的顶点位置、颜色计算公式为
总结
- 基于网格的图像变体算法运算结果的质量取决于最初建立的源图像A和目标图像B的四边形网格的质量
- 四边形网格越精细，则变体结果的图像质量一般也越高
- 四边形网格应当包含图像的尖点和拐点等关键点
- 四边形网格一般要求是凸四边形，如果出现凹四边形，则可进一步分成凸四边形
- 缺点：算法灵活性不够
自由变形
FFD基本思想：
- 自由变形方法在变形过程中并不是直接操作几何模型，而是把几何模型嵌入到变形空间，然后通过操作变形空间来使得嵌入其中的几何模型发生变形
- 模仿泥巴或塑料等柔性体的变形，将需要变形的物体或物体的某部分嵌入到类似于泥巴或塑料的柔性体中，然后假设物体也是非常柔软的，会随着物体外围柔性体的变形而发生变形
FFD实现：
- 将物体全部或部分嵌入到网格中
- 然后通过对网格的变形（即改变网格顶点的位置）控制物体的变形
- 二维网格对应 grid
- 三维网格对应 lattice
二维自由变形具体算法
- 将物体嵌入到一个平行四边形
- 将平行四边形沿着边的方向划分为𝑚×𝑛个网格，也称为控制网格
- 各个格子的顶点称为网格的控制顶点
- 当移动这些控制顶点时，网格发生变形，从而带动嵌入的物体的变形
算法关键在于求得物体任意点
令
三维自由变形
三维自由变形可看作是二维自由变形的扩展
主要思想： ①将整个物体或物体所需要发生变形的部分嵌入到一个平行六面体中
②给平行六面体内部及其边界上的每个点分配一个固定的网格参数坐标
③通过移动控制顶点，引起物体的变形
网格参数坐标计算公式
四、基本光照模型
光源
光源(light source) –任意发出辐射能量的对象
光源可以是发光体和反射体的混合
光源属性：
- 位置
- 发射光颜色
- 发射方向
- 光源形状
光源分类
点光源–指一个无限小的点，所有光向四周平均地散射光
适用范围：
- 比对象小得多的光源
- 离场景不是太近的大光源
无穷远光源
- 光源在无限远放射
- 在任何位置，放射方向都是一致的，可以模拟类似太阳的光线
辐射强度衰减
光强度随着光源距离
离光源距离为
问题：
- 接近光源时，会产生过大的强度变化
- 当
很大时，变化又太小
改进
方向光源和投影效果
对局部光源稍加修改可产生方向光源
方向光源–对象位于光源的方向范围
Vlight – 光源方向的单位向量
Vobj – 光源位置到一个对象位置的方向向量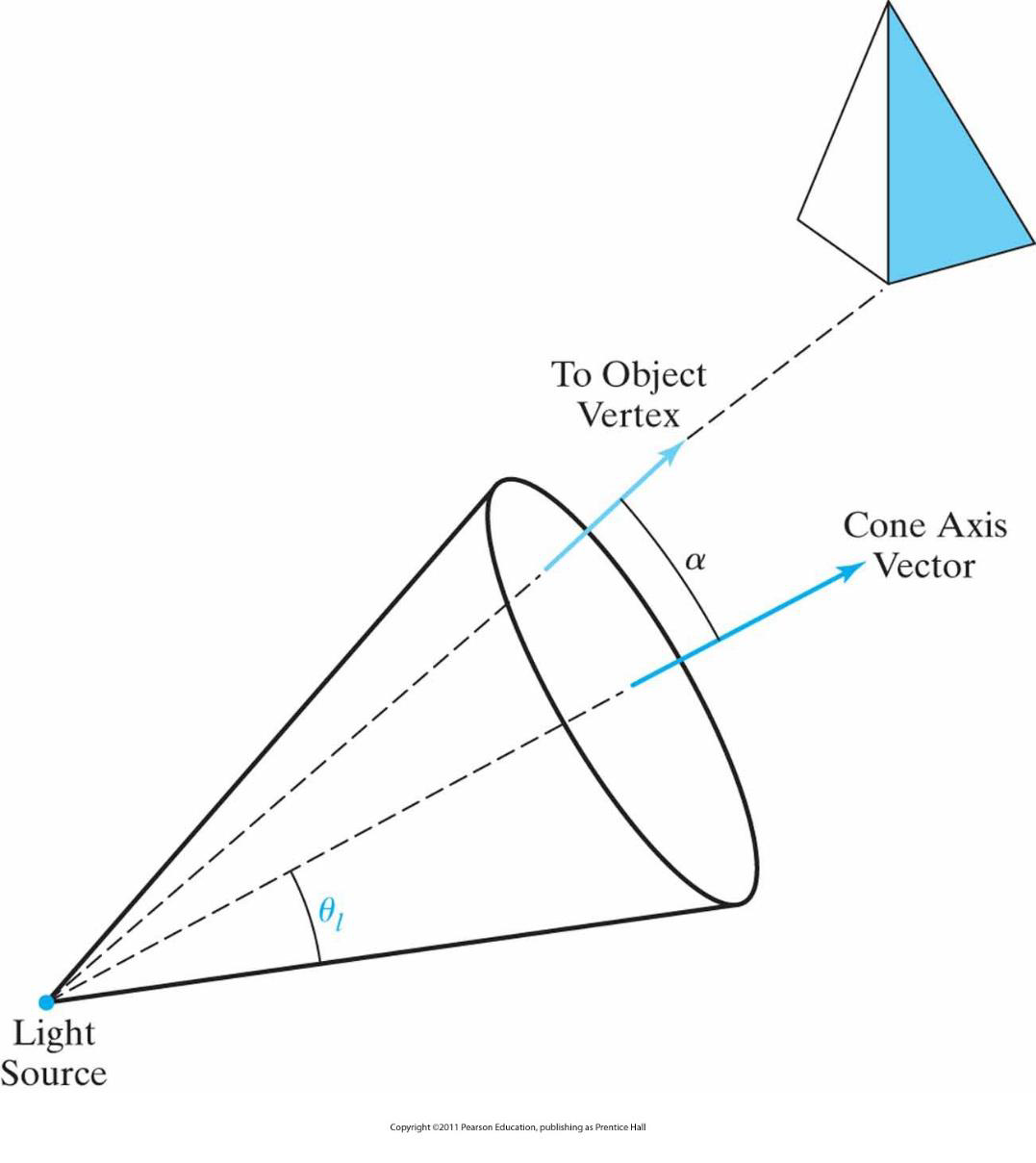 
角强度衰减
沿着圆锥轴光强最大，离开时强度减弱
方向光源角强度衰减函数：
基本光照模型
反射
- 漫反射：表面将光向各个方向发散出去（粗糙表面）
- 镜面反射：反射光汇集中在一部分区域（光滑表面）
环境光（背景光）-场景中各个表面的反射光生成的光照效果
- 环境光：设定场景一般亮度级
环境光
入射光在各个方向以相同强度发散而与观察者位置无关
对于背景光效果，假定每一表面都使用对场景设定的环境光
物体在该点处光强度为
漫反射
当强度为Il的光源照射一个表面时，从该光源来的入射光总量依赖于表面与光源的相对方向
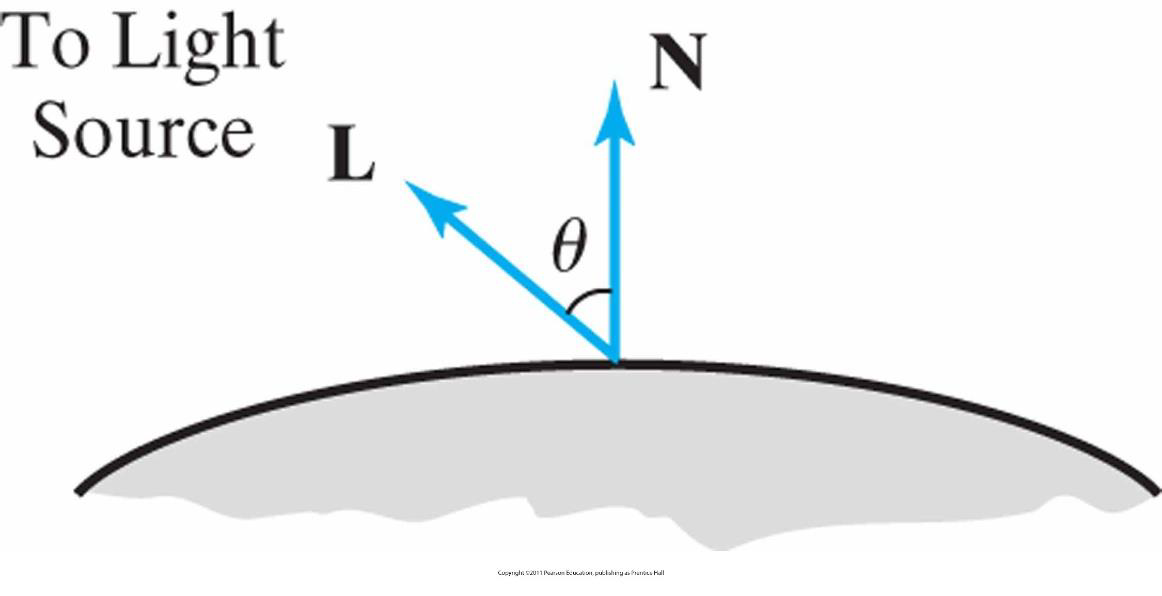
漫反射光强度
L 为指向点光源的单位方向向量
镜面反射
在光滑表面上看到的高光
- 镜面反射是由接近镜面反射角的一个汇聚区域内，入射光的全部或绝大部分成为反射光所导致的
- V–指向视点的单位向量
- 理想的反射体–V与R的夹角为0，仅当V与R重合时才能观察到反射光
反射方向分布在向量 R 周围的有限范围内
- 较光滑表面的镜面反射范围较小
- 粗糙的对象表面有较大的反射范围
Phong 镜面反射模型
镜面反射光强度与
使用向量L与V间的半角向量H来计算镜面反射范围，可以得到简化的 Phong
模型：
只需要用
替代 经验性估算
来替代
总结
对于单点光源，光照表面上某点处的漫反射和镜面反射为
透射模型
透明表面–可透过该表面看到其后面的东西，如窗玻璃
透明对象表面同时产生反射光和折射光
折射角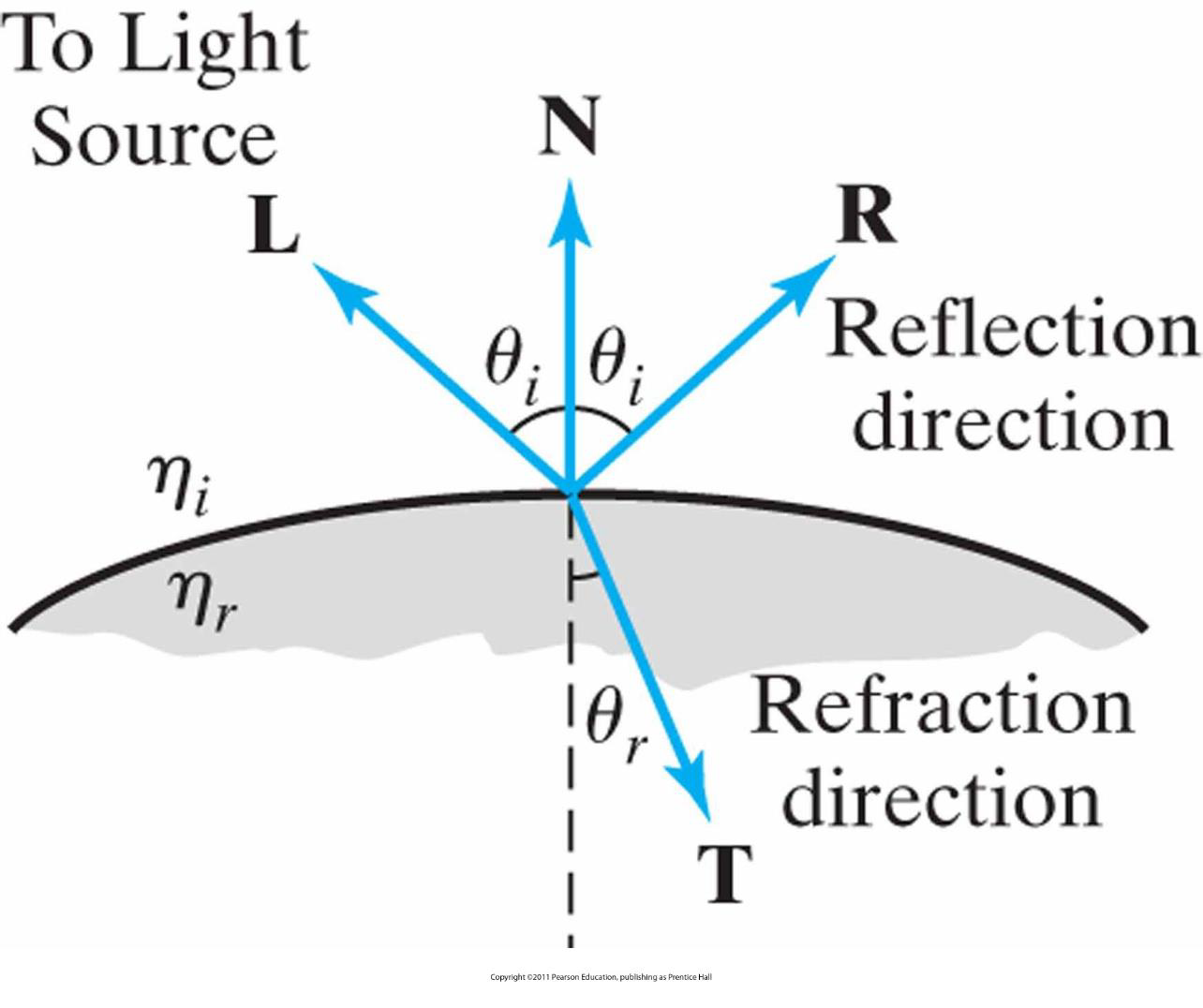 
折射方向向量 T
- 不考虑折射导致的路径平移
- 各对象间的折射率不变
- 折射角=入射角
对象表面的折射光强
对象表面的总光强
五、全局光照
局部光照
- 计算对象表面和射向它的光线之间的交点处光照强度
- 只考虑特定对象（光源）和直接射向它的光线
全局光照
- 从其他对象反射出来的光线
- 产生更真实的光照效果
- 需要付出大量额外计算的代价
两大算法：
①光线跟踪法：从视点出发做出经过图像平面上每个像素的光线并射回到场景中，以此为基础来计算表面的明暗效果
②辐射度算法：更加准确的模型。考虑场景中光源与对象表面间辐射能量的传递来计算光强度
光线跟踪算法
光源跟踪(ray tracing) –跟踪光线在场景中的反射和折射，并计算他们对光强的作用 优点：
- 生成高度真实感图形
缺点：
- 计算量大的惊人
光线跟踪算法是一种高度视相关的方法，因为进入场景并被跟踪的光线是从投影参考点出发的，如果观察者位置发生了变化，光线就全部都要重新计算和跟踪 如果场景中任何一个对象的位置改变了，就会引起光线反射的过程改变，从而导致部分甚至所有的光线必须重新计算
基本光线跟踪算法
为光线跟踪算法建立一个投影参考点在z轴、投影平面为xy平面的坐标系统
从投影参考点出发，穿过每个像素中心进入场景
计算与该光线相交的所有表面，找到最近的交点（可见面）
计算该光线在此交点上反射和折射光强度
构造二叉光线跟综树
构造停止条件：
- 该光线不和任意表面相交
- 该光线与一个光源相交且该光源不是一个反射面
- 该树达到最大允许深度
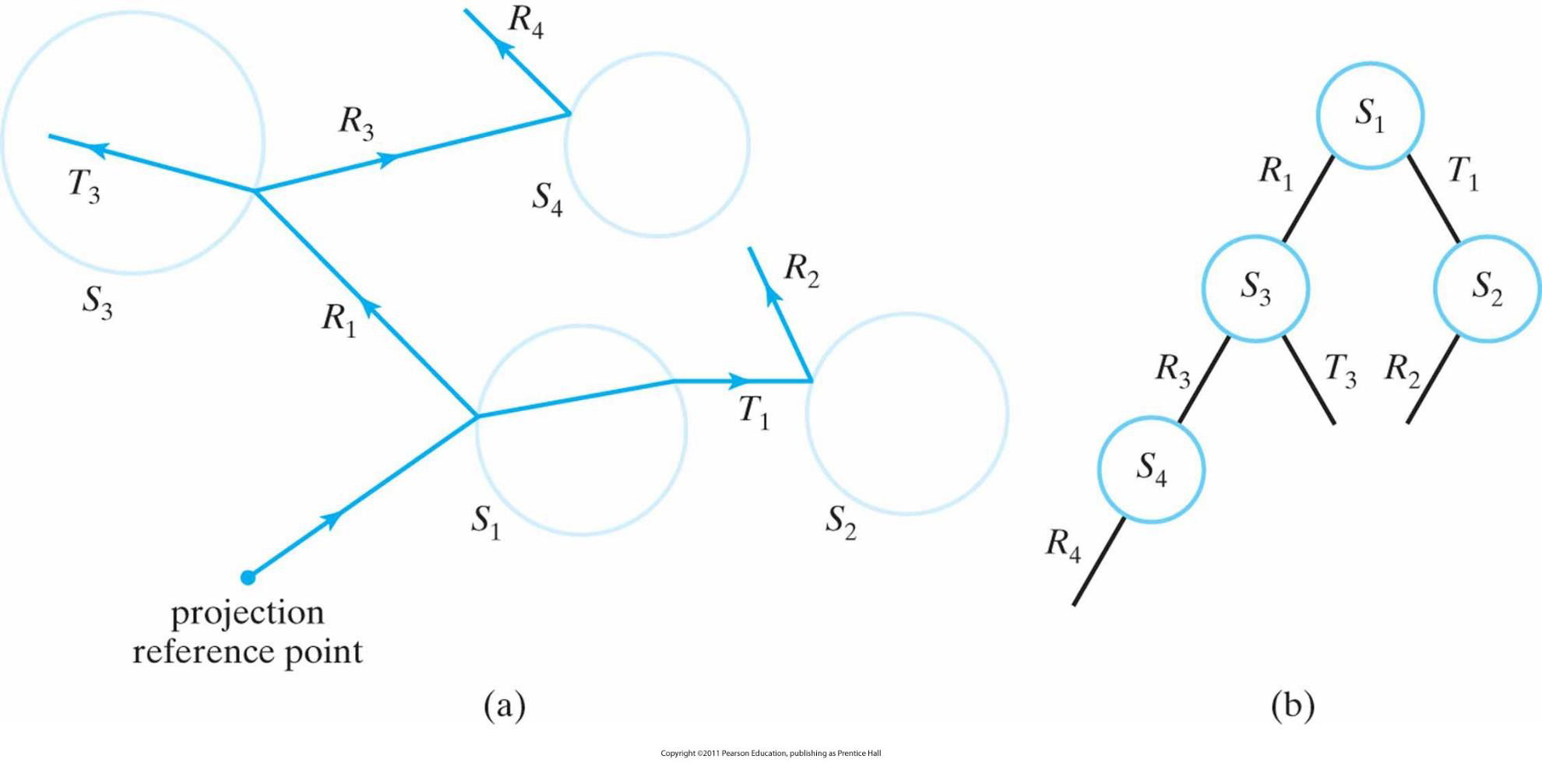
一个像素的二叉树建立完毕，从树的末端开始累积强度贡献
树的每一节点的表面强度因离开父节点表面的距离而衰减并加入到父节点表面的强度中
光强度逐级衰减
待解决问题
漫反射物体表面反射光方向任意
采用 Monte Carlo 方法采样
仍然存在问题：
- 计算开销太大！
- 反射光呈指数级增长
解决方案：
反射光线数N=1
结果：画面充满噪声
对每条光线多次采样
SPP (samples per pixel)增加
无限循环
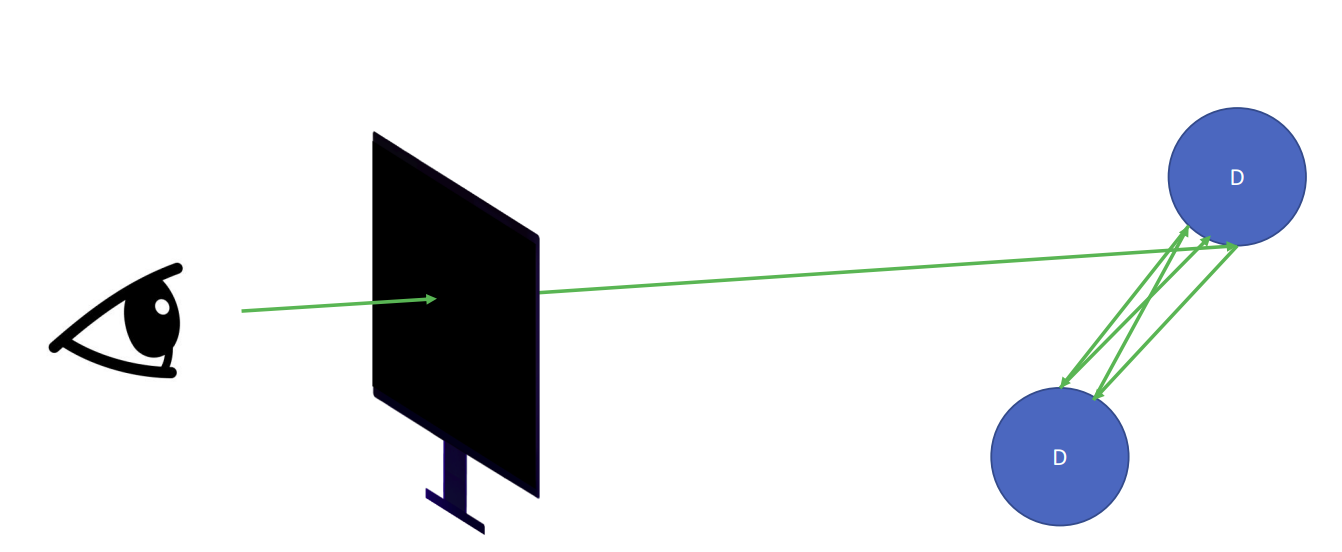
解决方案：
在第二次反射回来结束
但是存在能量损失
解决方案：
- 俄罗斯轮盘赌Russian Roulette
光线与对象表面求交计算
光线由初始位置
光线-球面求交
球面上任意点
若
光线-多面体求交
多面体求交计算相对于球体复杂得多，一般利用包围体进行求交测试
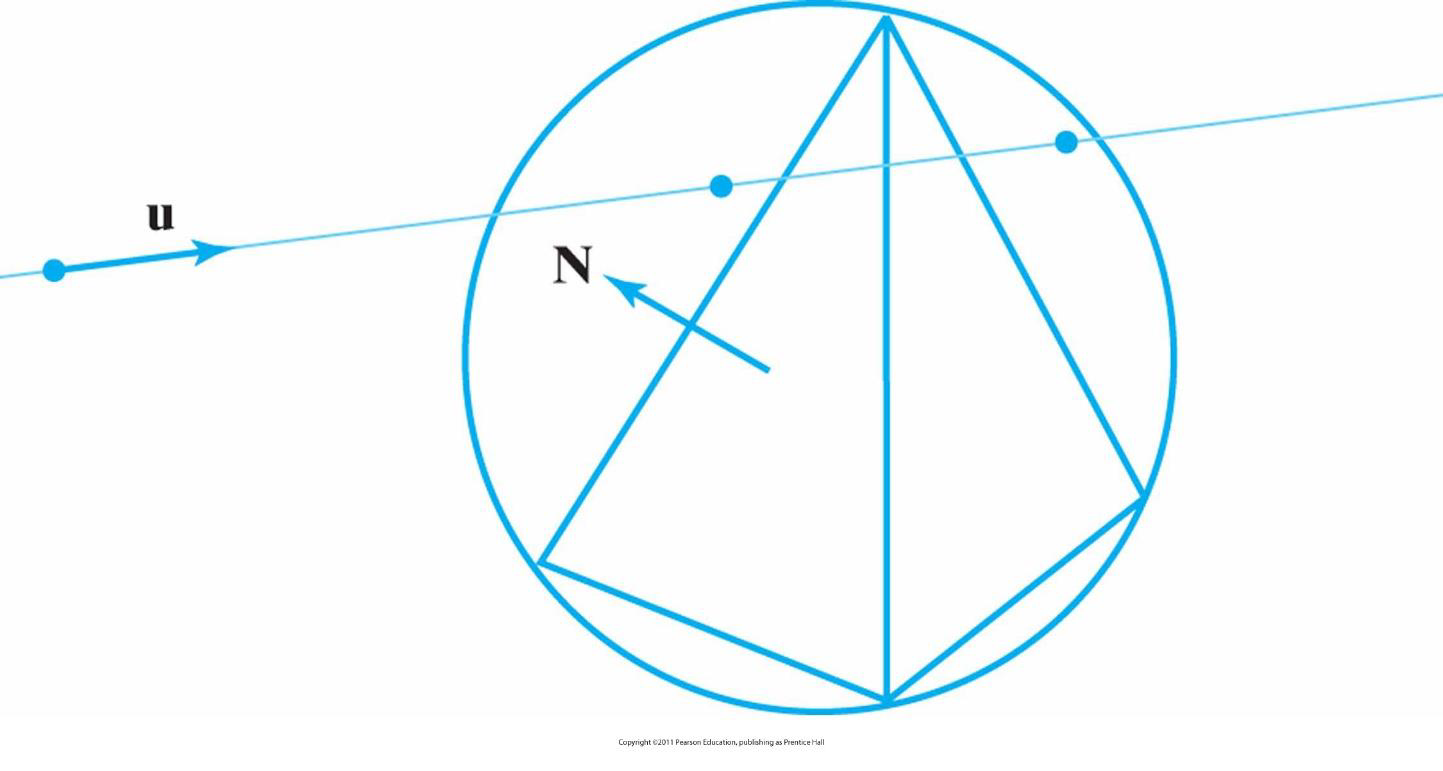
具体来说：
若光线与包围体相交，则需测试：
其中， 为多面体表面法向量 通过上述测试找到多面体的前表面
求解所有前表面与光线交点
减少对象求交计算量
方法一：将相邻对象用一个包围盒（包围球）包起来
- 测试光线与包围体的交点
- 如果没有交点，则无须对被包围对象进行求交测试
- 分层包围盒（扩展）：将几个包围体包在一个更大的包围体中，首先测试最外层的包围体，然后根据需要逐个测试各层的包围体
方法二：空间分割法
- 将整个场景包含在一个立方体中
- 将立方体逐次分割直至每个子立方体所包含的对象表面或表面数目小于等于一个预定的最大值
- 跟踪穿过立方体的光线，仅需对包含表面的单元执行求交测试。光线所交的第一个对象表面记为可见面
- 该过程继续直到找到一个相交的对象表面或光线射出包围场景的立方体
六、纹理映射
纹理映射（texture mapping）-纹理模式映射到对象表面上
种类：
- 2D映射（2D mapping）
- 3D映射（3D mapping）
方法：
- 建立像空间和纹理空间映射关系
- 纹理坐标0到1.0
2D 映射
Map shape: planar
Map shape 是一个平面
对于物体上每个点
Map Shape: Cylinder
用一个形状将物体包裹起来，如圆柱体：
物体表面坐标
–对应于 texture map 中 坐标 –对应于 texture map 中 坐标
Map Shape : Sphere
球体：
- 物体表面坐标
转换为球面坐标 - 纬度–对应于 texture map 中
坐标 - 经度–对应于 texture map 中
坐标
Map Shape：Box
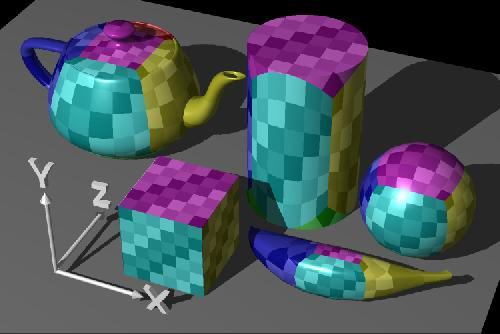
3D 映射
利用对象每个点
等同于将物体从一个石块中雕刻出来
函数
凹凸映射
纹理图案的光照细节的设定通常与场景中光照方向无关
纹理映射无法模拟粗糙表面物体
凹凸映射（bump mapping）：通过修改物体表面法向量来影响表面阴影的计算
使用扰动函数并在光照模型计算中使用扰动法向量
令
增加一个小的扰动函数（凹凸函数）
方向上增加凹凸效果：
①定义一个解析表达式
②定义一个凹凸表来快速查找
七、关节动画
基本概念
关节–如果两个刚体互相连接且能够发生相对运动，则这两个刚体的关联部分称为关节
常见的关节
旋转关节
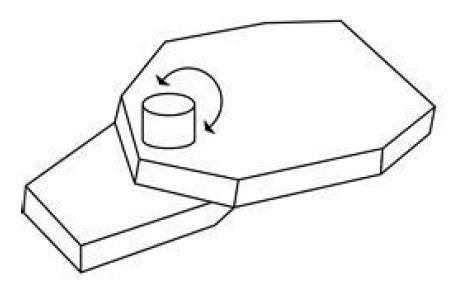
滑动关节
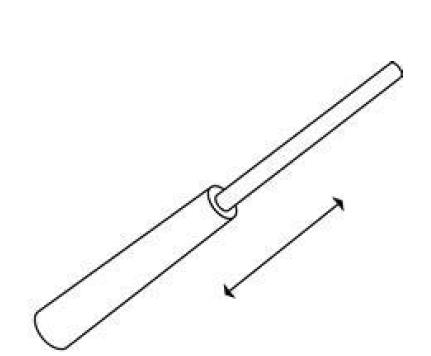
关节链–将一系列依次相连的刚体通过关节连接而成的开链
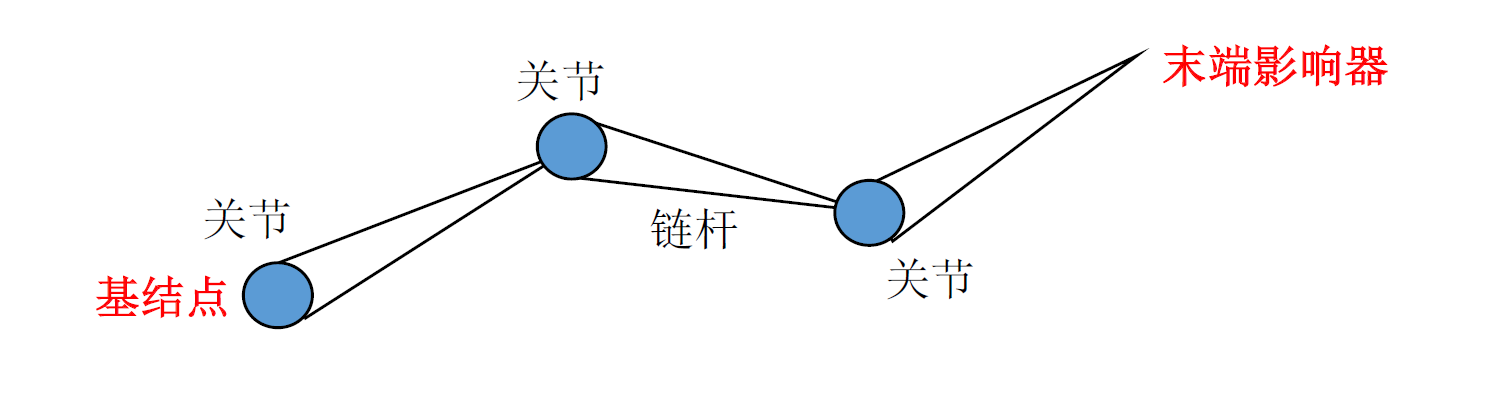
链杆–关节链中每一段刚体
基结点–关节链的起点
末端影响器–关节链的自由末端(End effector)
状态空间–关节链结构所有可能形态的向量空间
状态向量–状态空间中的向量
关节链结构的自由度（Degree of freedom -DOF）–状态空间的维度，完全确定关节链结构状态所需的独立变量个数
正向运动学
研究如何从给定的状态向量计算各个链杆的位置（包括各个关节的位置），尤其是末端影响器的位置
动画师通过直接指定关节处的关节运动参数来控制物体的运动
二维的关节链为例，各个关节链均在一个平面上运动
- 各个链杆均只能绕着各自的起点运动
- 设关节链的基节点位置固定在全局坐标系的原点
- 链杆的方向为从链杆的起点到终点的方向
三链杆关节链
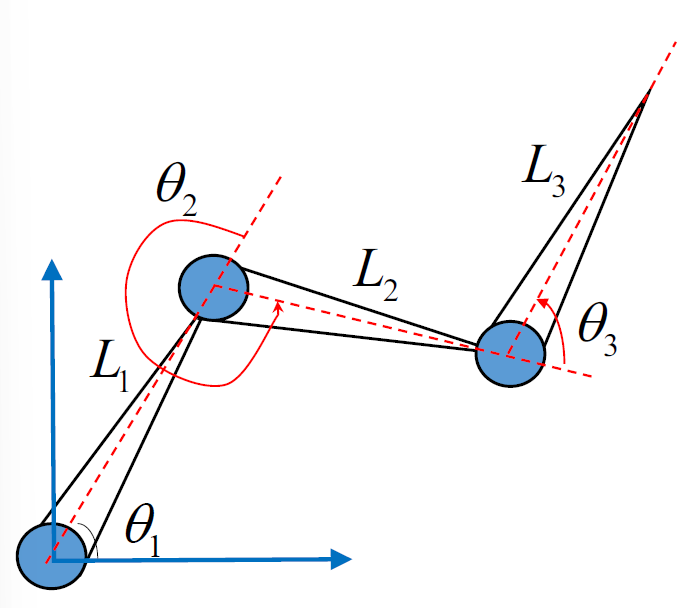
逆向运动学
逆向动力学研究的内容与正向运动学研究的内容恰好相反
逆向动力学是一种目标驱动技术，即研究如何从末端位置计算状态向量的位置
意义：动画设计者只需要控制末端位置，而不需要控制整个关节链结构，系统求解满足要求的关节，从而简化动画设计
方法
- 解析法求解简单系统：设法推导出具体的求解公式，并分析解的合理性，从而选取合理的解
- 如果关节链的逆向求解过于复杂，则直接采用一些数值计算方法进行求解，如Jacobian方案，CCD方案
大多数计算机动画中的相关问题，解析方案较复杂，不适合采用解析型求解方案 解决方法：
- 利用牛顿迭代法求解
即已知末端影响器的位置x和y，求解、2和。令
方程组的 Jacobian 矩阵
$$
其中
牛顿迭代法
求得矩阵
Cyclic-Coordinate Descent (CCD)
循环坐标下降：通过逐步调整关节角度，实现最小化末端影响器与目标位置之间的距离
方便快速
链杆
通过旋转多少度尽可能接近目标位置 ？ 旋转
度达到新位置 链杆
通过旋转多少度尽可能接近目标位置 ？ 旋转
度达到新位置 链杆
通过旋转多少度尽可能接近目标位置 ？ 上述过程不断迭代，当 C 与 P 接近或者达到一定的迭代次数
层次结构建模
单个关节链结构通常不足以描述人体或动物等角色的运动
通常将人体或动物等角色分解成若干个关节链结构，并形成树状的层次结构，称为骨架树
首先将人体骨骼抽象成为关节和链杆组成的模型
然后选取其中的某个关节作为根节点，建立骨架树
骨架树建立后，通过关节链的正向运动学和逆向运动学求解骨架树的正向和逆向运动
八、物理动画基础
什么是物理动画？
追溯现象本身的物理根源，借助其本身较为精确的物理描述才能真实再现其外在的视觉现象
基于物理的计算机动画的迅速发展：
计算机硬件的不断发展，计算能力不断增强
算法的不断改进
在市场方面，不管是电影特效，还是视频游戏，人们对于基于物理的计算机动画的需求也很强烈
物理动画包含哪些内容？
物理模拟技术
- 刚体动力学模拟(rigid body dynamics simulation)
研究刚性物体在外力作用下的运动表现形式
- 刚体：在任何情况下其形状和大小都不发生任何变化的物体，即在刚体内任何两点的距离永远保持不变 刚体动力学模拟多涉及物体的平移、旋转以及碰撞的效果
- 柔体动力学模拟(soft body dynamics simulation)
用于逼真再现变形物体（或软组织）的运动状态
- 柔体：对象上任意两个点的相对距离不固定，但是相对距离变化通常满足一定的约束条件 柔软的有机材料，如肌肉，脂肪，头发和植被，以及其它可变形的无机材料如衣服和织物 计算机动画中提供的模拟方法只提供直观可信的仿真，而不涉及精确的科学或工程模拟
- 流体动力学模拟(fluid dynamics simulation)
- 流体： –某些物体无法采用刚体或者柔体模拟的方法进行模拟，而这些物体在自然界中颇为常见 –此类对象的运动规律往往比较难于描述。比如：水流、云彩以及火焰等对象的运动描述 –如何对这些特殊对象运动建模以及找到其在某些特定条件下的近似运动方案是流体动力学模拟考虑的问题
- 碰撞侦测(collision detection)
- 当物体在环境中运动时，如果该环境并非无限空旷，那么对象迟早会和周围环境的对象发生碰撞。在计算机动画中，如果未对此采取任何处理，那么就会出现对象穿越现象
- 为了使得生成动画真实可信，需要准确模拟对象间的交互行为。比如刚体间碰撞，柔体间碰撞（布料与环境中对象的碰撞，头发之间相互碰撞）以及流体之间相互碰撞
实现物理动画的关键因素？
根据已知物理运动规律来模拟物体运动
动画制作更注重运动的整体质量，不涉及物体的位置和方向的精准控制
可信度胜过精准度
计算机动画产生原理
要生成一段运动物体的动画，只需要间隔小段时间重新计算这个物体的位置并在画面上绘制物体，当画面连续播放时，就能看到连续运动的物体了
生成物体运动状态的信息是计算机动画的关键
运动学模拟
已知物体
- 位置矢量p(t)
- 速度矢量v(t)
- 加速度矢量a(t)
计算下一个模拟时间的状态：
①我们不知道如何积分这些量？
②我们不知道
无法用蒙特卡洛法求积分
可采用数值积分的方式来处理
显式（前向）欧拉积分
辛欧拉积分
优势：
- 物体能量（动能+势能）长期维持稳定
- 在某个值附近波动
- 依赖于时间步长
隐式（后向）欧拉
优势：
- 物体能量（动能+势能）一直减小(因为在用
) 近似，舍去了第二项及以后的值
考试题：求解
解： 移项，得 于是得
改进的欧拉
实例：一个简单的物理动画
实现一个简单的自由落体运动 已知物体的信息如下：
初始位置：
初始速度： 初始加速度：
运动模糊
产生原理
照相机或者摄像机能够记录下影像都是依赖于曝光
曝光是指场景中的光线投射在胶片上，引起化学反应，最终产生图片
但是如果在曝光的过程中，场景发生变化或者长时间曝光，则就会产生模糊的画面
运动模糊出现在长时间曝光或场景内的物体快速移动的情形里。
优点
- 在动画中加入运动模糊后能使运动变得更平滑，场景更逼真
- 缺乏运动模糊是计算机动画不真实的原因之一，因为计算机产生的图像“棱角分明”，很注目，以致削弱了运动效果
模拟方法
保留每帧绘图结果
每帧画一个半透明的黑色长方形，将前面绘图结果变暗
九、粒子系统
特殊的视觉效果或者现象，如：
- 火、爆炸、烟、水流、火花、落叶、云、雾、雪、尘、流星尾迹或者发光轨迹
- 这些现象用其它传统的计算机动画渲染技术难以实现模拟
物体具有共同的特征：
- 在外观上呈现出一定的不规则性、不确定性和随机性
- 同一物体在不同时刻会具有不同的形状，甚至差别很大
- 常用的欧几里得几何学方法很难再适用于这一类物体外观形态的描述
- 物体内部运动规律具有一定的复杂性，其运动过程较难把握和控制，特别是当受到外力作用时，其运动的不确定性和随机性更加突出
什么是粒子系统？
粒子系统是最实用的过程动画技术之一，是影视特技游戏、图形学中生成视觉特效的一种主要方法。
粒子系统采用了一套完全不同于以往的造型、绘制方法来构造、绘制景物，造型和动画巧妙地连成一体。
景物被定义为由成千上万个不规则的、随机分布的粒子所组成，而每个粒子均有一定的生命周期，它们不断改变形状、不断运动。
随后被广泛应用于模拟模糊不规则物体。Reeves 首先应用粒子系统模拟了星球燃烧时的景象，并在其后对烟花进行了模拟
应用
- 云彩
- 烟雾
- 流动的水(瀑布、水花)
- 爆炸、碎片、尘土
- 火(火花)
- 喷泉
- 烟花
- 下雪、下雨、落叶
- 大群体
- 草、发丝
粒子系统的定义
粒子系统可看作由大量的微小物质组成的系统，这些微小物质按一定规则运动（变化）这些微小物质称为粒子（particle）
粒子的定义
粒子带有运动状态；
- 粒子是独立的，粒子之间互不影响(不碰撞、没有力) 。由于粒子之间的碰撞计算量很大并且对于大多数模拟来说没有必要，所以很少使用粒子之间的碰撞；但不是绝对！
- 粒子有生命周期，生命结束后会消失；
- 粒子形状可以设为任意形状，比如可设定为球体，三角形等形状
- 粒子若处于聚集状态，粒子不向其它粒子投射阴影
- 粒子只向其它环境投射阴影
- 粒子不反射光
粒子的基本属性
- 运动属性
- 位置
- 速度
- 加速度
- 渲染效果
- 生命值
- 粒子颜色
- 粒子大小
粒子系统生成过程
- 生成（发射）粒子
- 模拟粒子状态变化
- 模拟粒子受力运动
- 模拟粒子老化
- 模拟粒子与环境的交互（如：碰撞）
- 渲染粒子
粒子系统更多的应用
更复杂的粒子系统
对于每一帧，根据一个控制的随机过程生成粒子：
- 用户可控制每帧的平均粒子数和其概率分布
- 粒子数可以是时间的函数
方法一：
粒子数:
- 其中，m为平均粒子数;
- rand() 返回
之间的随机数 - v 为方差；
方法二：
粒子数:
- 其中，m为平均粒子数;
- rand() 返回
之间的随机数 - v 为方差；
- A 为物体的屏幕面积(Screen Area)
- 在该方法中，新生成的粒子数以依赖于物体在屏幕上的投影面积。
颜色和透明度可以是时间（其剩余的生命周期、其高度等）的函数
形状可以是速度的函数
粒子上的力
粒子对力做出反应
粒子上的力可以是一元力(unary force)、粒子的偶力(particle pair force)或环境力
一元力
- 重力(Gravity)
- 粘性阻力(viscous drag)
粒子的偶力
- 可表示为弹簧阻尼器
环境力
- 根据粒子与环境的关系来得到
粒子的绘制
- 把每个粒子当成一个点光源
- 把每个粒子绘制成一个小的图元；
- 把映射到同一像素的颜色相加；
- 把每个粒子建模为一个带纹理的广告牌(textured billboard)
- 纹理多边形面向视点
- 把每个粒子看成元球，绘制整个元球系统(用于模拟水等液态效果)
粒子的碰撞检测
判断一个粒子是否与物体发生碰撞
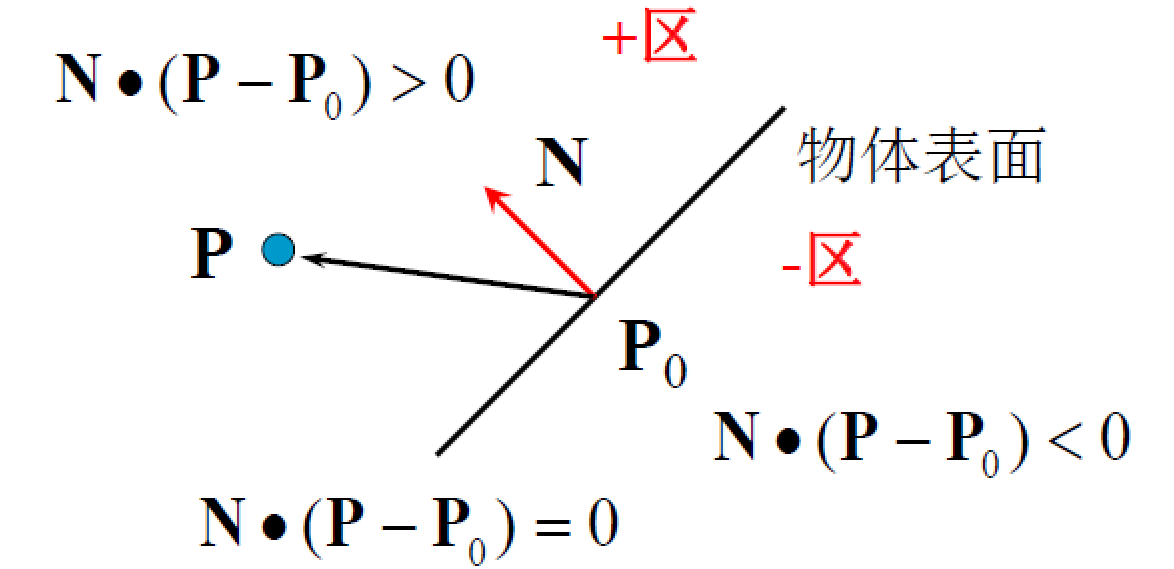
当且仅当
十、弹性网络
什么是弹性对象?
通过施加在对象上的力（如挤压或者拉伸），可改变物体的形状
有可能随着力的消失返回初始形态
对象上的两个点的相对距离不固定，但是相对距离变化满足一定的约束条件
哪些是弹性对象？
- 布料
- 头发
- 果冻
如何实现弹性对象?
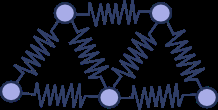
将一个弹性对象看作由无数个质点构成的物体，质点之间有边作为连接
那么这个弹性对象能够发生形变，一定是因为连接质点的边具有发生弹性形变的性质
弹性网络
弹簧-质量模型
- 当外部力作用于对象时，作用力会使得质点产生运动，由于质点之间通过弹簧连接，质点之间相互运动产生弹力并作用于其它质点；同时作用力还会反馈到初始移动的质点
- 作用力将沿弹簧边传播，进而使对象富有弹性，并在顶点之间产生持续的相对偏移
- 将对象的顶点作为质点，连接质点的边作为弹簧进行建模
- 质点一般具有质量，质点质量大小总和等于对象质量大小
- 弹簧静止时长度可定义为原始边长
- 弹性系数由用户设定
弹簧-质量-阻尼系统
- 由于弹簧在没有阻力的情况下，会持续摆动，那么这就会造成弹性对象在受到外力作用后不断发生形变，永不停止
- 为了防止这种现象出现，我们在弹簧上另外附加一个阻尼系统，使得弹簧弹力逐渐减弱
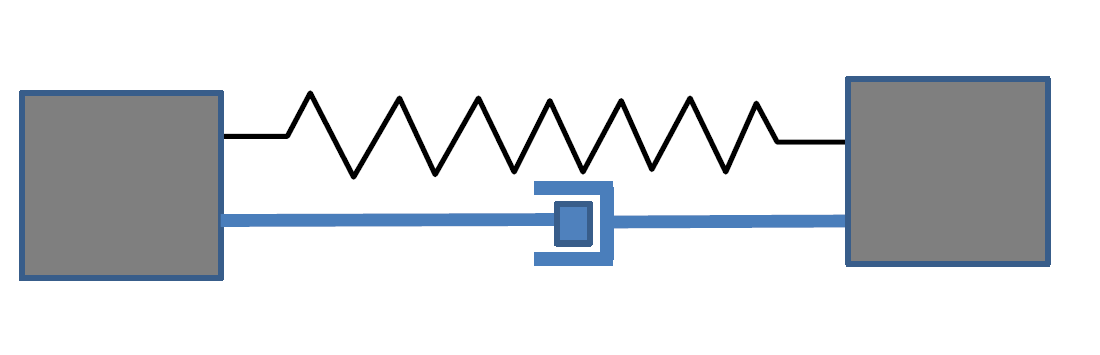
简单弹性对象的实现–摆动的绳子
已知：
: 弹性系数 : 相邻质点相距平衡位置的位移 ：弹簧位于稳定状态时，相邻质点间距离 ：阻尼系数
弹力：
推导步骤：
- 将质点速度值从三维空间投影至一维空间（质点连线方向）
- 在质点连线方向上计算弹力、阻力
复杂弹性对象的实现
假设绳子一端固定悬挂起来，另一端可自由运动，绳子一部分与地面接触
地面以上部分：
- 重力以及空气阻力的影响
地面上的质点：
- 在地面运动时，质点与地面产生相互作用，如质点与地面摩擦力
- 质点与地面冲撞时，损失部分动能，同时地面对其产生反作用力
重力
空气摩擦力
当物体在某一介质以某一速度行进时，介质的黏度会阻止物体运动
所施加的力大小一般与物体速度成正比，方向与速度相反。如：空气摩擦力计算大小和速度相关：
质点与地面摩擦力
– 只考虑动摩擦力 – 动摩擦力近似计算: 已知物体速度向量
质点与地面相互作用力
质点与地面冲撞时，能量会被地面吸收 用一个反作用力（Absorption
force）来近似表示能量的损失
应用
1D：绳子->头发
- 《GPU Gems》hair animation
- 爱丽丝的发丝-《爱丽丝惊魂记：疯狂再临》
2D：布料
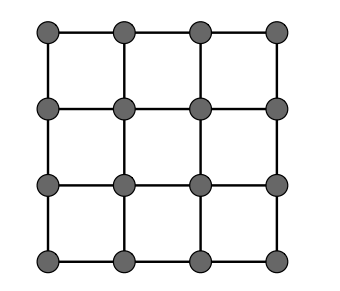
3D：果冻、面团
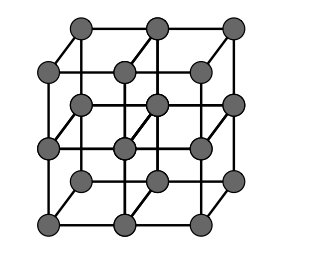
弹簧-质量模型改进
弹性物体运动受到其结构影响 现有结构存在问题：
- 无法抵抗错切方向上施力
- 无法抵抗折叠形变
改进方案：
增加抵抗错切方向上施力的弹簧
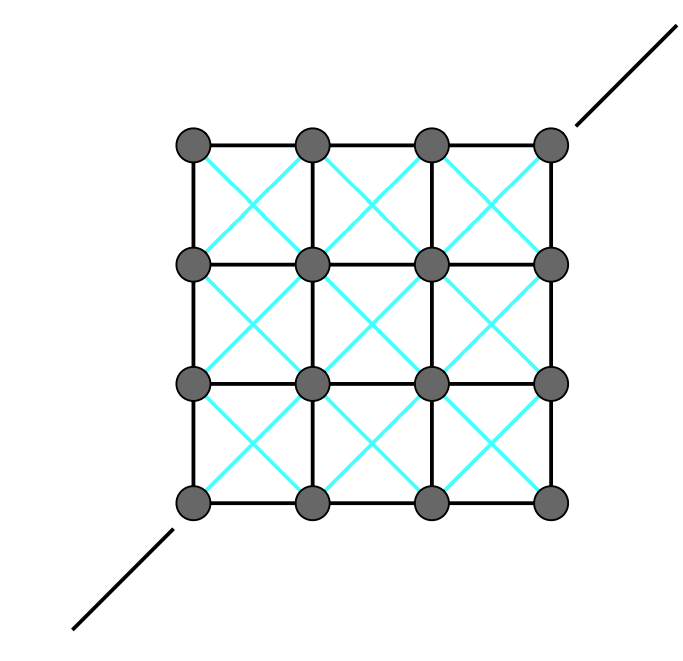
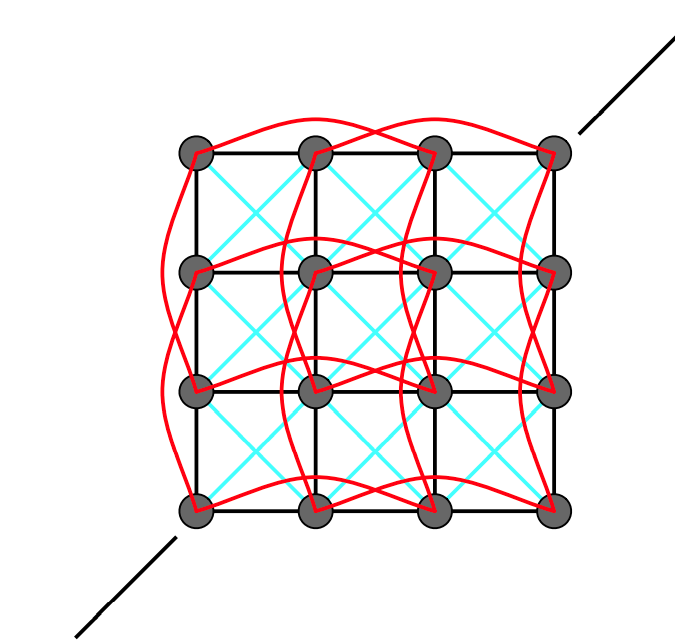
解决折叠形变
红色弹簧弹性系数弱于蓝色弹簧
十一、高级物理效果
布料建模
布料模拟方法
布料建模
模拟质点运动
计算质点受力
除了弹力以外其他受力：重力…
根据受力更新质点运动状态
- 韦尔莱法积分
渲染
韦尔莱法（Verlet）积分
韦尔莱积分算法是一种用于求解牛顿运动方程的数值方法。1967 年法国物理学家 Loup Verlet 将其应用于分子动力学计算，从此韦尔莱算法流行起来，被广泛应用于分子动力学模拟以及视频游戏中
韦尔莱算法的优点：
- 数值稳定性比简单的欧拉方法高很多
- 可以简单地加入各种约束(constraint)
Verlet 方法在精度与速度之间取得了前所未有的平衡，越来越多游戏使用这种方法来模拟物体以及人体运动效果
在实际使用当中，适当修改系数，含简单阻尼效果
约束
假设质点位置向量为
松弛法
求解方程：
给定
减少开方运算时间
泰勒公式
十二、水面模拟
真实感水体的渲染和模拟，一直是计算机图形学和游戏开发领域的核心难点之一。
水体渲染中，最核心的部分为波形的模拟技术，即如何模拟出逼真的水面波浪的流动变化。
按时间分布，近50年水体波形渲染的主流技术发展可以总结列举如下：
- 凹凸纹理贴图（Bump Mapping）[Schachters1980]
- 正弦波（Sinusoids Wave）[Max 1981]
- 分形噪声（Fractal noise）[Perlin1985]
水面模拟步骤
水面建模
模拟水面运动
- 物理模型描述水面的状态，比如能够描述水面的波动、涟漪等
水面渲染
- 特殊的光学效果，如反射、折射以及菲捏尔效果
菲捏尔效果
视线垂直于表面时，反射较弱，而当视线非垂直表面时，视线与表面法线夹角越大，反射越明显
水面建模
水面外观与地形外观非常相似，不同点在于水面外观高度是随着时间变化的
- 首先将平面看作普通的均匀网格，每一个网格点(x, y)对应一个水面高度值
- 水面是动态的随着时间变化的，因此其网格高度值是一个与时间相关的函数H (x, y, t)
模拟水面运动
假设水面开始静止不动
在某一位置有一振动源作简谐振动，振动产生的波向四周传播
水面在任意位置
根据该振源信息以及时间
简单模型（2D）
假设某振源位于一维坐标系下原点处
- 振动产生的波沿着x轴方向传播
- 位于
处点在时刻 水面高度为 与 时刻传播到此处的波的幅度有关
要知道位于
- 推导出位于振源在
时刻振幅 为波从振源传播到 所需时间
振源处发出的波沿着
在
完整模型（3D）
二维平面上某点
振幅（Amplitude——A）：平面到波峰的距离
波转播速度（Speed——S）：波峰每秒移动距离
波浪传播方向（Direction——D）：垂直于波阵面的向量
法向量
已知水面上任意点坐标$$ 其中
波浪的种类
定向波浪：
- 波的传播方向D为定值
圆形波浪：
- 每一点处波浪传播方向需要重新计算
- 若已知振源位置向量C，位于网格点(x, y)处的波浪传播方向D为：
两种波浪适用场合：
- 对于大面积水体（如海面），定向波浪比较适用于表达受风吹动的水面
- 对于小的水池，通常产生波动的振源通常不是风，较常见的如水滴滴落，此时用圆型波浪模拟水面比较合适
多个振源
让水面运动更加真实：
- 通常水面运动看作一系列正弦波的叠加
- 已知根据第i个正弦波推导的水面方程为：
更真实的模型
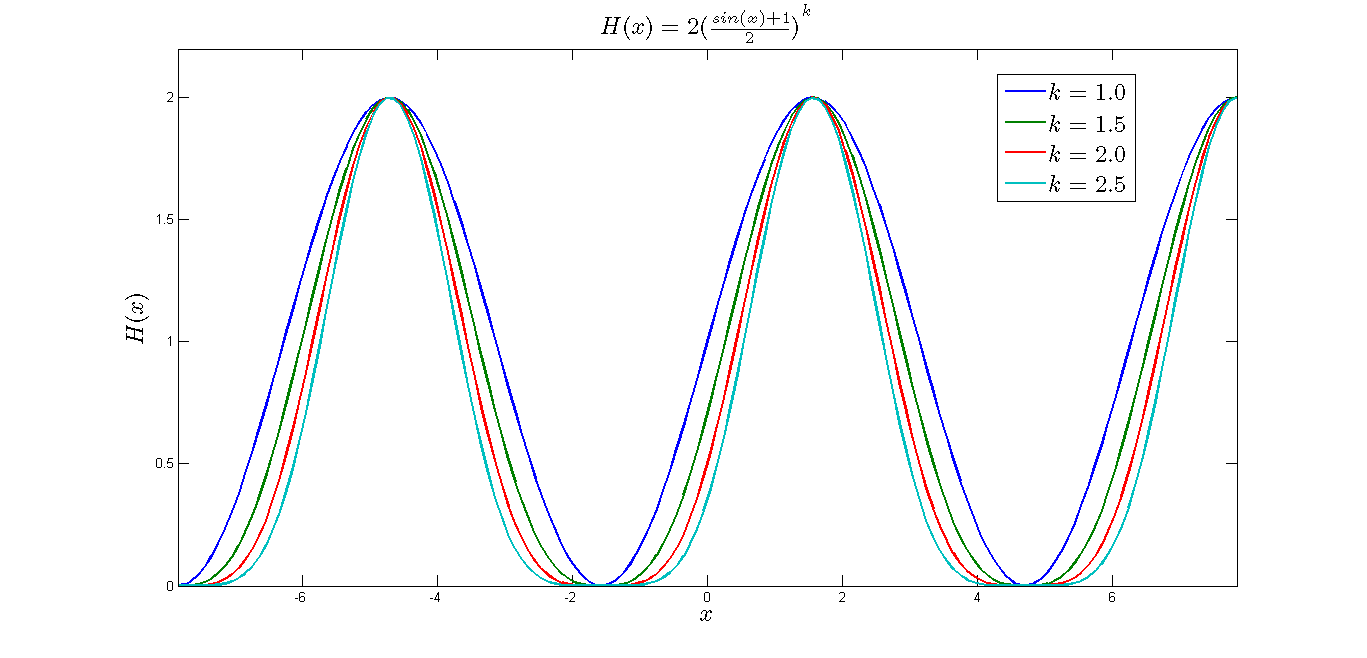
幂指数模型
$$ k 值越大，波峰更突兀，波谷更宽
Gerstener Waves
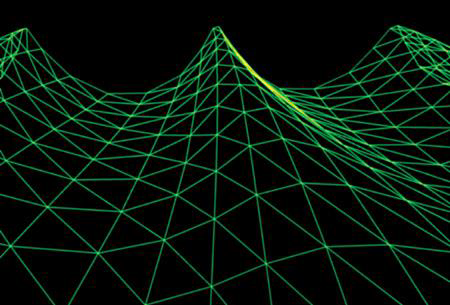
每个网格点（x, y）在X和Y方向发生了位移，而高度值是相同的
当
$$ 给出非常尖锐的波峰
在模拟时应避免将
法线计算
参数设置
对于深水区的波浪，波长和波相位满足如下关系